英国 13+ 究竟考什么?
13+ 例解
13+ 是学生在 Year 8(英国 8 年级)时进行(即 12, 13 岁左右)的一种升学考试,供孩子在 13+ (即九年级, 亦即入读 GCSE 前一学年)时入学作准备。在英国本地就读小学的孩子们在申请私立学校时只需要提供在小学升初中的考试(Common Entrance)成绩即可,并不需要进行学校的入学考试。而没有参加小升初考试的海外学生则可参加学校设立的入学考试,学校会制定符合该学校收生标准的试卷,考试内容与小升初考试大致一样,但形式上可能有点区别。大多学校都愿意提供历年试题让学生练习。 13+ 入学考试每学年有三个主要考试时间,分别在 11 月,1 月和 5/6 月。主要考试内容一般为数学,英语和科学,除此之外考生还可以选择一系列补充考试,例如二外(包括中文),历史、地理等等。
我们首先来看 13+ 的数学考试。相对 11+ ,这里会有知识要求上的补充以及更大的灵活性运用性。
例题 1 Merchant Taylor’s School

麦钱特泰勒斯学校 Merchant Taylor’s School 给出的样本试卷分为可用计算器和不可用计算器两套;这道题属于可用计算器的试题。学生需要对幂和开方的运算、负数的性质、四舍五入都有熟练的掌握。
例题 2Merchant Taylor’s School

这道题的分值并不高,图形也很直观,并不算难。但是,它却是大学数学课程里概率论(Probability)的基础;概率论是对这一类基础题的抽象化,复杂化和理论化。计算白球/黑球被拿到的概率,其实就是计算白球/黑球所占的比例;理解了这一点,每道题就迎刃而解了。
例题 3 Dulwich College
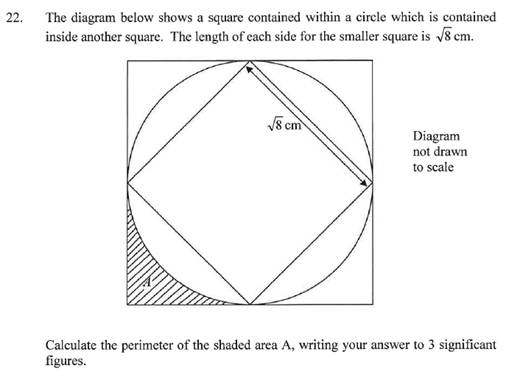
这是一道较为基础的几何题,考察不规则图形的面积计算,方法就是利用规则图形来推算。通过小正方形的边长利用勾股定理可以得到对角线长,即可推出圆形的半径和大正方形的边长,继而算出圆形的面积和大正方形的面积,那么阴影部分面积即为大正方形面积减去圆形面积后所得数值的四分之一。需要提示的是,在解题时一定要把思路步骤充分展示出来。
例题 4 Dulwich College
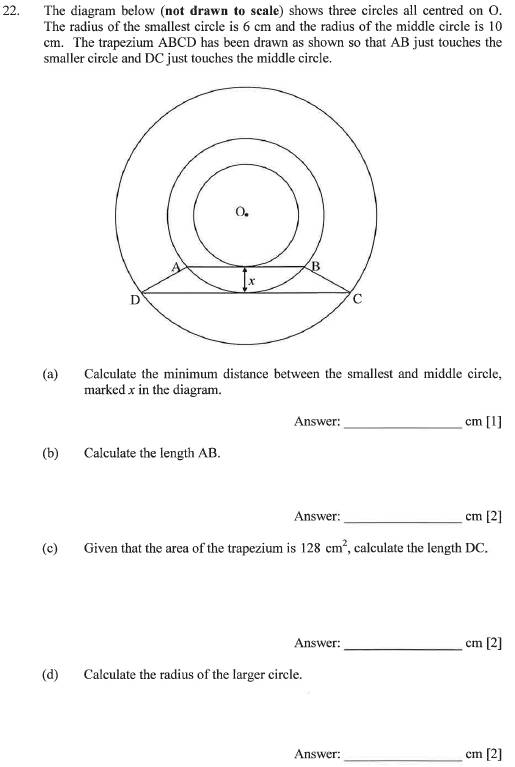
这道题所涵盖的知识点要丰富很多,不仅有同心圆的直半径性质,梯形的性质和面积,最重要也是较难的知识点还在于切线的性质。这道题的解答关键在于,第一,圆心到切点联结的线段是与过该切点的切线垂直的;而过一点的垂线有且只有一条,这两条知识结合可以计算出 AB 和 CD 两条切线上切点的距离;第二,直线外一点到直线的最短距离就是该点到直线的垂线长短,由这一点我们可以确定,两切点之间距离就是两个同心圆的最短距离。这些都是(a)题的隐藏理论知识。
(b)题的关键是,连接 OA,构成一个直角三角形,利用勾股定理计算直角边的长度。
(c)题需要考生了解梯形的面积计算公式。
(d)题,同样利用购股定理,连接 OD,塑造直角三角形。
接下来我们看看英语试题。
例题 1 Dulwich College

这是一道细节和词汇题。学生不仅需要对句子理解透彻,与上下文进行联系,并且需要有丰富的词汇量。
例题 2 Merchant Taylor’s School

这是麦钱特泰勒斯学校(Merchant Taylor’s School)的作文题,一般会给几个话题供考生选择最擅长发挥的。在写作中要脱颖而出,不仅要展现丰富的词汇量和表达方式,精湛的讲故事技巧,还需要有一定的创意和突破性。